Answer:
1. The required information are
The average annual bonuses,
 received by employees from company A
received by employees from company A
The average annual bonuses,
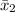 received by employees from company B
received by employees from company B
The standard deviation, σ₁, of the average annual bonuses for employees from company A
The standard deviation, σ₂, of the average annual bonuses for employees from company A
The number of employees in company A, n₁
The number of employees in company B, n₂
2. The null hypothesis is H₀:
 -
-
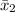 ≤ 100
≤ 100
The alternative hypothesis is Hₐ:
 -
-
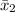 > 100
> 100
Explanation:
1. The required information are
The average annual bonuses,
 received by employees from company A
received by employees from company A
The average annual bonuses,
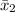 received by employees from company B
received by employees from company B
The standard deviation, σ₁, of the average annual bonuses for employees from company A
The standard deviation, σ₂, of the average annual bonuses for employees from company A
The number of employees in company A, n₁
The number of employees in company B, n₂
2. The null hypothesis is H₀:
 -
-
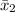 ≤ 100
≤ 100
The alternative hypothesis is Hₐ:
 -
-
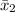 > 100
> 100
The z value for the hypothesis testing of the difference between two means is given as follows;
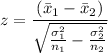
At 0.5 level of significance, the critical
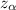 = ± 0
= ± 0
The rejection region is z >
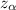 and z < -
and z < -
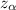
Therefore, the value of z obtained from the relation above more than or less than 0, we reject the null hypothesis, and we fail to reject the alternative hypothesis.