Question

Employees from A and company B receive annual bonuses. What information would you need to test the claim that the difference in annual bonuses is greater than $100 at the 0.5 level of significance? Write out the hypothesis and explain the testing procedure in details

Answer 1

1. The required information are

The average annual bonuses,
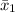`\bar {x}_1` received by employees from company A

The average annual bonuses,
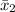`\bar {x}_2` received by employees from company B

The standard deviation, σ₁, of the average annual bonuses for employees from company A

The standard deviation, σ₂, of the average annual bonuses for employees from company A

The number of employees in company A, n₁

The number of employees in company B, n₂

2. The null hypothesis is H₀:
`\bar {x}_1` -
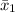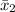`\bar {x}_2` ≤ 100

The alternative hypothesis is Hₐ:
`\bar {x}_1` -
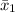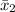`\bar {x}_2` > 100

Explanation:

1. The required information are

The average annual bonuses,
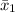`\bar {x}_1` received by employees from company A

The average annual bonuses,
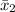`\bar {x}_2` received by employees from company B

The standard deviation, σ₁, of the average annual bonuses for employees from company A

The standard deviation, σ₂, of the average annual bonuses for employees from company A

The number of employees in company A, n₁

The number of employees in company B, n₂

2. The null hypothesis is H₀:
`\bar {x}_1` -
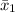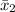`\bar {x}_2` ≤ 100

The alternative hypothesis is Hₐ:
`\bar {x}_1` -
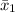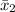`\bar {x}_2` > 100

The z value for the hypothesis testing of the difference between two means is given as follows;

`z=\frac{(\bar{x}_(1)-\bar{x}_(2))}{\sqrt{(\sigma_(1)^(2) )/(n_(1))-(\sigma _(2)^(2))/(n_(2))}}`

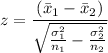
At 0.5 level of significance, the critical
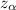`z_\alpha` = ± 0

The rejection region is z >
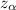`z_\alpha` and z < -
`z_\alpha`

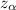
Therefore, the value of z obtained from the relation above more than or less than 0, we reject the null hypothesis, and we fail to reject the alternative hypothesis.