Answer:
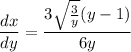
General Formulas and Concepts:
Algebra I
- Terms/Coefficients
- Functions
- Function Notation
Calculus
Derivatives
Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Product Rule]:
![\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)](https://img.qammunity.org/2021/formulas/mathematics/high-school/s1om3rzcnorfu9si84gajpl5k6jeoialwk.png)
Implicit Differentiation
Explanation:
Step 1: Define
Identify
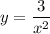
Step 2: Differentiate
- Rewrite Function:
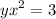
- [Implicit Differentiation] Basic Power Rule [Product Rule]:
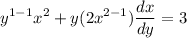
- Simplify:
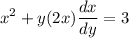
- Isolate
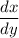 term:
term:
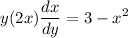
- Isolate
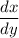 :
:
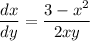
- Substitute in x²:
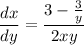
- Simplify:
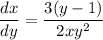
- Substitute in x:
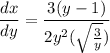
- Simplify:
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Derivatives
Book: College Calculus 10e