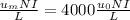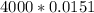Answer:
a) B = 0.0151 T
b)

c)
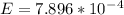
d)

Step-by-step explanation:
Given:
Diameter, d = 2.5 cm convert to meters = 0.025 m
Length, L = 30.0 cm convert to meters = 0.3 m
Number of turns, N = 300
Current, I = 12 A
a) Let's use the formula below to find the magnetic field.
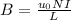
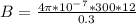
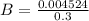
B = 0.0151 T
b) Given a radius, r = 1.00 cm, let's convert it to meters = 0.01 m
Let's use the formula below to find magnetic flux.
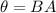
where
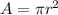
Therefore,
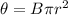
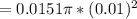

c) Given that the current in the solenoid uniformly goes from 12 A to 10 A in 0.001 seconds, the EMF generated will be:

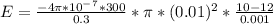
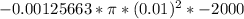
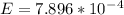
d) Let's use the formula: