Answer:
1.Corresponding angles theorem
2.Linear postulate
3.By the definition of supplementary angles
Explanation:
We are given that
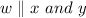 is a transversal.
is a transversal.
We have to prove
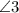 and
and
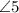 are supplementary
are supplementary
Proof:
1.Given that
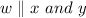 is a transversal.
is a transversal.
We know that

Reason:Corresponding angles theorem
Therefore,
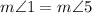
by the definition of congruent.We also know that, by definition, angle 3 and angle 1 are a linear pair.
Therefore, they are supplementary by linear pair postulate
By the definition of supplementary angles
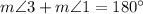
Now, we can substitute
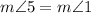
Then, we get
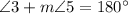
Therefore, by the definition of supplementary angles,angle 3 and angle 5 are supplementary