Answer:
y= (2/3)x - 4
Explanation:
To answer this you'll want to use the slope intercept form of a line:
y= mx + b
So to solve essentially you just have to find the values for m and b
- m represents the slope of the line
- b is the y-intercept (the point where the line crosses the y-axis)
You can figure that b = -4 because the line will cross the y-axis when x = 0, and you are given the point on the line (0,-4), where x is equal to 0.
Now to find the slope of the line, since you are given two points on the line you will want to use the slope equation:
slope =
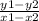
So you can assign each of the two points a number (1 or 2) where its values are equal to (x1, y1) or (x2, y2). It does not matter which point gets which number.
In this example:
We will assign the point (6,0) to be (x1, y1),
and we will assign the point (0, -4) to be (x2, y2)
So we end up with the following:
m=
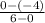
m=
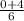
m=
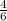
Simplify the fraction:
m =

From there you just substitute in for m and b into the slope intercept equation