Question

Which linear equation includes the points
(6,0) and
(0, – 4)?

Answer 1

y= (2/3)x - 4

Explanation:

To answer this you'll want to use the slope intercept form of a line:

y= mx + b

So to solve essentially you just have to find the values for m and b

- m represents the slope of the line

- b is the y-intercept (the point where the line crosses the y-axis)

You can figure that b = -4 because the line will cross the y-axis when x = 0, and you are given the point on the line (0,-4), where x is equal to 0.

Now to find the slope of the line, since you are given two points on the line you will want to use the slope equation:

slope =
`(y1-y2)/(x1-x2)`

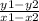
So you can assign each of the two points a number (1 or 2) where its values are equal to (x1, y1) or (x2, y2). It does not matter which point gets which number.

In this example:

We will assign the point (6,0) to be (x1, y1),

and we will assign the point (0, -4) to be (x2, y2)

So we end up with the following:

m=
`(0- (-4))/(6-0)`

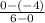
m=
`(0+4)/(6)`

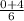
m=
`(4)/(6)`

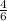
Simplify the fraction:

m =
`(2)/(3)`

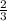
From there you just substitute in for m and b into the slope intercept equation

Answer 2

The linear equation that includes the points (6, 0) and (0, -4) is y = (2/3)x - 4.

To find the linear equation that includes the points (6, 0) and (0, -4), we use the slope-intercept form of a linear equation: y = mx + b, where m is the slope and b is the y-intercept.

First, calculate the slope (m) using the given points (6, 0) and (0, -4): m = (-4 - 0) / (0 - 6) = 2/3.

Now, use one of the points (6, 0) to find the y-intercept (b): 0 = (2/3)(6) + b, resulting in b = -4.

Therefore, the linear equation is y = (2/3)x - 4.