Question

Why do we think 0! = 1?

Answer 1

`4!=4*3*2*1=24\\3!=3*2*1=6\\2!=2*1\\1!=1\\0!=?`

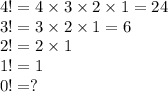
Notice that when we go from 4! to 3! , we divide by 4.

(Because
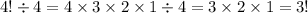`4!/ 4 = 4*3*2*1/4=3*2*1=3!` the 4's cancel)

And when we go from 3! to 2! , we divide by 3, and etc.

We can use this pattern to see why 0! = 1.

`4!=4*3*2*1=24\\3! = 4!/4=24/4=6\\2!=3!/3=6/3=2\\1!=2!/2=2/2=1\\0!=1!/1=1/1=1`

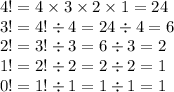
And so by following the pattern, we determine that 0! = 1

-------------------------------

Note:

There are no factorials of negative numbers, and we can use the pattern to show why:

`0!=1\\-1!=0!/0=1/0=???!!??!?`

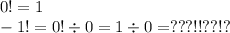
You can't divide a number by 0, therefore -1! doesn't exist, so -2! doesn't exist and so on. So you can't do the factorial of any negative number.

(Or at least there no real solutions to negative factorials)

------------------------