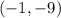Answer:
We have axis of symmetry in
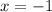
The vertex point is
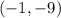
The roots by factoring are
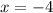

Explanation:
We have the function:
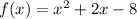
Factoring the quadratic equation:

When

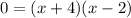
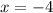

The vertex point is
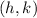
From the equation, we have

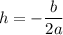
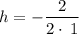
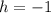
We also got the axis of symmetry
In order to find
 just use the
just use the
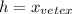 :
:
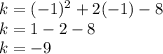
Once
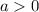 , we have the minimum at
, we have the minimum at