Answer:
x = -1 <--- axis of symmetry
(-1, -9) <-- vertex
2, -4 (or, in my old precalc class we wrote our roots as (2,0) and (-4,0)) <--- roots
Explanation:
a) Axis of symmetry equation is defined as
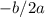 = x (i memorized this)
= x (i memorized this)
Quadratic equation form:
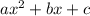
And our original equation:
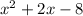
So..
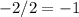
So our axis of symmetry is at x = -1,
b) now vertex point can be found by plugging this value back into our original equation.
y =
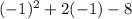
y = 1 - 2 - 8
y = - 9
So our vertex is at (-1, -9)
c) Finally, lets factor
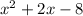 = 0 (when finding the roots, set y = 0, because we are trying to find where we cross the x-axis)
= 0 (when finding the roots, set y = 0, because we are trying to find where we cross the x-axis)
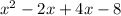 = 0
= 0
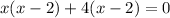
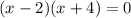
x = 2; x = -4 <--- Roots