Question

Y=x^{2} +2x-8 determine the axis of symmetry, the vertex point and find the roots by factoring

Answer 1

x = -1 <--- axis of symmetry

(-1, -9) <-- vertex

2, -4 (or, in my old precalc class we wrote our roots as (2,0) and (-4,0)) <--- roots

Explanation:

a) Axis of symmetry equation is defined as

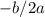`-b/2a` = x (i memorized this)

Quadratic equation form:

`ax^2+bx+c`

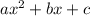
And our original equation:

`x^2+2x-8`

So..

`-2/2 = - 1`

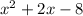
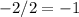
So our axis of symmetry is at x = -1,

b) now vertex point can be found by plugging this value back into our original equation.

y =
`(-1)^2+2(-1)-8`

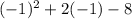
y = 1 - 2 - 8

y = - 9

So our vertex is at (-1, -9)

c) Finally, lets factor

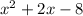`x^2+2x-8` = 0 (when finding the roots, set y = 0, because we are trying to find where we cross the x-axis)

`x^2-2x+4x-8` = 0

`x(x-2) + 4(x-2) = 0`

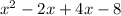`(x-2)(x+4)=0`

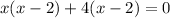
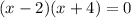
x = 2; x = -4 <--- Roots