Answer:
h = 16 mm
Explanation:
Th volume of the prism is:
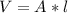 (1)
(1)
Where:
V. is the volume of the triangular prism = 416 mm³
A. is the area of the prism = ?
l: is the large of the prism = 4 mm
The area of the triangular face of the prism is:
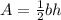 (2)
(2)
Where:
b: is the base of the triangular face = 13 mm
h: is the height of the triangular face = ?
From equation (1) we have:
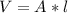
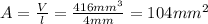
Now, using equation (2) we can find the height of the triangular face:
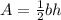
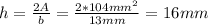
Therefore, the height of the triangular face is 16 mm.
I hope it helps you!