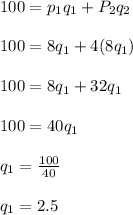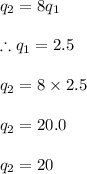Answer:
The value of "
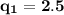 ".
".
Step-by-step explanation:
Given value:
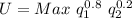
Differentiate the above equation with respect of
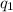 , which will give
, which will give
 as follows:
as follows:

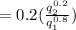
Differentiate the equation with respect of
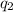 , which will give
, which will give
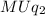 as follows:
as follows:
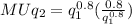
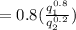
for balancing the equation
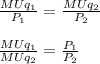

Calculate the value of
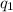 and
and
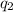 as follows:
as follows: