Question

Let X and Y be independent normal random variables with distributions X „ Np1, 3q and Y „ Np0, 4q. Let W " 1 2X ´ Y ` 6. (a) Identify the distribution W. (b) Find the probability PpW ą 6q.

Answer 1

Explanation:

Here we have,

E(X) = 1, var(X) = 3, E(Y) = 0, var(Y) = 4

Since X and Y has normal distribution so W will also have normal distribution with mean

E(W) = E(05X-Y+6)

= 0.5E(X) - E(Y) +6

= 0.5* 1 -0+ 6

= 6.5

and variance

Var(W) = Var(0.5X-Y+6)

= 0.25Var(X)+Var(Y)

= 0.25 * 3 + 4

= 4.75

(b)

The z-score for W = 6 is

`z=(6-6.5)/(√(4.75) ) \\\\=-0.23`

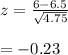
The required probability is:

P(W>6) = P(z > -0.23)

= 0.5910