Question

The position function of a particle moving along a coordinate line is given, wheresis in feet andtis in seconds.

s(t)= t/t^2+4, t>=0

a. Find the velocity and acceleration functions.
b. Find the position, velocity, speed, and acceleration at time t=1.
c. At what times is the particle stopped?
d. When is the particle speeding up? Slowing down?
e. Find the total distance traveled by the particle from time t=0 to time t=5

Answer 1

a) s = (4-t)/(t^2+4)^2, a(t) = (2t^3-24t)/(t^2+4)^3

b) s = 0.2ft, v = 0.12 ft/s, a = -0.176 ft/s^2

c) t = 2s

d) slowing down for t < 2, speeding up for t > 2

e) 0.327 ft

Explanation:

The position function of a particle is given by:

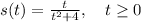`s(t)=(t)/(t^2+4),\ \ \ t\geq 0` (1)

a) The velocity function is the derivative, in time, of the position function:

`v(t)=(ds)/(dt)=((1)(t^2+4)-t(2t))/((t^2+4)^2)=(4-t^2)/((t^2+4)^2)` (2)

The acceleration is the derivative of the velocity:

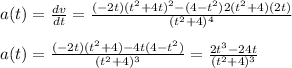`a(t)=(dv)/(dt)=((-2t)(t^2+4t)^2-(4-t^2)2(t^2+4)(2t))/((t^2+4)^4)\\\\a(t)=((-2t)(t^2+4)-4t(4-t^2))/((t^2+4)^3)=(2t^3-24t)/((t^2+4)^3)` (3)

b) For t = 1 you have:

`s(1)=(1)/(1+4)=0.2\ ft\\\\v(1)=(4-1)/((1+4)^2)=0.12(ft)/(s)\\\\a(1)=(2-24)/((1+4)^3)=-0.176(ft)/(s^2)`

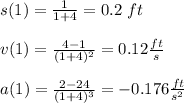
c) The particle stops for v(t)=0. Then you equal equation (2) to zero ans solve the equation for t:

`v(t)=(4-t^2)/((t^2+4)^2)=0\\\\4-t^2=0\\\\t=2`

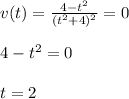
For t = 2s the particle stops.

d) The second derivative evaluated in t=2 give us the concavity of the position function.

`(d^2s)/(dt^2)=a(2)=(2(2)^3-24(2))/((2^2+4)^3)=-0.062<0`

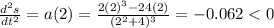
Then, the concavity of the position function is negative. For t=2 there is a maximum. Before t=2 the particle is slowing down and after t=2 the particle is speeding up.

e) Due to particle goes and come back. You first calculate s for t=2, then calculate for t=5.

`s(2)=(2)/(2^2+4)=0.25\ ft`

`s(5)=(5)/(5^2+4)=0.172\ ft`

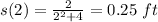
The particle travels 0.25 in the first 2 seconds. In the following three second the particle comes back to the 0.172\ ft. Then, in the second trajectory the particle travels:

0.25 - 0.127 = 0.077 ft

The total distance is the sum of the distance of the two trajectories:

s_total = 0.25 ft + 0.077 ft = 0.327 ft