Answer:
a) s = (4-t)/(t^2+4)^2, a(t) = (2t^3-24t)/(t^2+4)^3
b) s = 0.2ft, v = 0.12 ft/s, a = -0.176 ft/s^2
c) t = 2s
d) slowing down for t < 2, speeding up for t > 2
e) 0.327 ft
Explanation:
The position function of a particle is given by:
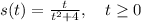 (1)
(1)
a) The velocity function is the derivative, in time, of the position function:
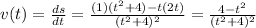 (2)
(2)
The acceleration is the derivative of the velocity:
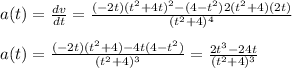 (3)
(3)
b) For t = 1 you have:
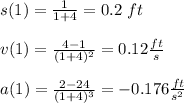
c) The particle stops for v(t)=0. Then you equal equation (2) to zero ans solve the equation for t:
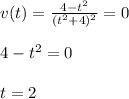
For t = 2s the particle stops.
d) The second derivative evaluated in t=2 give us the concavity of the position function.
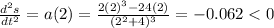
Then, the concavity of the position function is negative. For t=2 there is a maximum. Before t=2 the particle is slowing down and after t=2 the particle is speeding up.
e) Due to particle goes and come back. You first calculate s for t=2, then calculate for t=5.
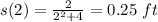
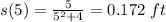
The particle travels 0.25 in the first 2 seconds. In the following three second the particle comes back to the 0.172\ ft. Then, in the second trajectory the particle travels:
0.25 - 0.127 = 0.077 ft
The total distance is the sum of the distance of the two trajectories:
s_total = 0.25 ft + 0.077 ft = 0.327 ft