Question

Harper's Index reported that the number of (Orange County, California) convicted drunk drivers whose sentence included a tour of the morgue was 506, of which only 1 became a repeat offender.

a. Suppose that of 1056 newly convicted drunk drivers, all were required to take a tour of the morgue. Let us assume that the probability of a repeat offender is still p= 1/596. Explain why the Poisson approximation to the binomial would be a good choice for r = number of repeat offenders out of 963 convicted drunk drivers who toured the morgue.

The Poisson approximation is good because n is large, p is small, and np < 10.The Poisson approximation is good because n is large, p is small, and np > 10. The Poisson approximation is good because n is large, p is large, and np < 10.The Poisson approximation is good because n is small, p is small, and np < 10. What is λ to the nearest tenth?

b. What is the probability that r = 0? (Use 4 decimal places.)
c. What is the probability that r > 1? (Use 4 decimal places.)
d. What is the probability that r > 2? (Use 4 decimal places.)
e. What is the probability that r > 3? (Use 4 decimal places.)

Answer 1

a. The Poisson approximation is good because n is large, p is small, and np < 10.

The parameter of thr Poisson distribution is:

`\lambda =np\approx1.6`

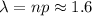
b. P(r=0)=0.2019

c. P(r>1)=0.4751

d. P(r>2)=0.2167

e. P(r>3)=0.0789

Explanation:

a. The Poisson distribution is appropiate to represent binomial events with low probability and many repetitions (small p and large n).

The approximation that the Poisson distribution does to the real model is adequate if the product np is equal or lower than 10.

In this case, n=963 and p=1/596, so we have:

`np=963*(1/596)\approx1.6`

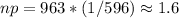
The Poisson approximation is good because n is large, p is small, and np < 10.

The parameter of thr Poisson distribution is:

`\lambda =np\approx1.6`

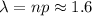
We can calculate the probability for k events as:

`P(r=k)=(\lambda^ke^(-\lambda))/(k!)`

b. P(r=0). We use the formula above with λ=1.6 and r=0.

`P(0)=1.6^(0) \cdot e^(-1.6)/0!=1*0.2019/1=0.2019\\\\`

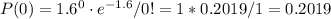
c. P(r>1). In this case, is simpler to calculate the complementary probability to P(r<=1), that is the sum of P(r=0) and P(r=1).

`P(r>1)=1-P(r\leq1)=1-[P(r=0)+P(r=1)]\\\\\\P(0)=1.6^(0) \cdot e^(-1.6)/0!=1*0.2019/1=0.2019\\\\P(1)=1.6^(1) \cdot e^(-1.6)/1!=1.6*0.2019/1=0.3230\\\\\\P(r>1)=1-(0.2019+0.3230)=1-0.5249=0.4751`

d. P(r>2)

`P(r>2)=1-P(r\leq2)=1-[P(r=0)+P(r=1)+P(r=2)]\\\\\\P(0)=1.6^(0) \cdot e^(-1.6)/0!=1*0.2019/1=0.2019\\\\P(1)=1.6^(1) \cdot e^(-1.6)/1!=1.6*0.2019/1=0.3230\\\\P(2)=1.6^(2) \cdot e^(-1.6)/2!=2.56*0.2019/2=0.2584\\\\\\P(r>2)=1-(0.2019+0.3230+0.2584)=1-0.7833=0.2167`

e. P(r>3)

`P(r>3)=1-P(r\leq2)=1-[P(r=0)+P(r=1)+P(r=2)+P(r=3)]\\\\\\P(0)=1.6^(0) \cdot e^(-1.6)/0!=1*0.2019/1=0.2019\\\\P(1)=1.6^(1) \cdot e^(-1.6)/1!=1.6*0.2019/1=0.3230\\\\P(2)=1.6^(2) \cdot e^(-1.6)/2!=2.56*0.2019/2=0.2584\\\\P(3)=1.6^(3) \cdot e^(-1.6)/3!=4.096*0.2019/6=0.1378\\\\\\P(r>3)=1-(0.2019+0.3230+0.2584+0.1378)=1-0.9211=0.0789`