Answer:
the rate of heat transfer into the wall is
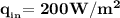
the rate of heat output is

the rate of change of energy stored by the wall is
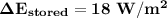
the convection coefficient is h = 4.26 W/m².K
Step-by-step explanation:
From the question:
The temperature distribution across the wall is given by :
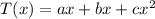
where;
T = temperature in ° C
and a, b, & c are constants.
replacing 200° C for a, - 200° C/m for b and 30° C/m² for c ; we have :
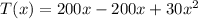
According to the application of Fourier's Law of heat conduction.

where the rate of heat input
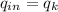 ; Then x= 0
; Then x= 0
So:

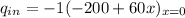
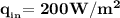
Thus , the rate of heat transfer into the wall is
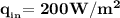
The rate of heat output is:
 ; where x = 0.3
; where x = 0.3
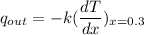
replacing T with
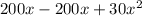 and k with 1 W/m.K
and k with 1 W/m.K

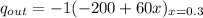
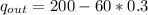

Therefore , the rate of heat output is

Using energy balance to determine the change of energy(internal energy) stored by the wall.
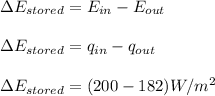
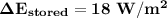
Thus; the rate of change of energy stored by the wall is
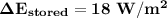
We all know that for a steady state, the heat conducted to the end of the plate must be convected to the surrounding fluid.
So:
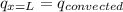
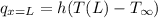
where;
h is the convective heat transfer coefficient.
Then:
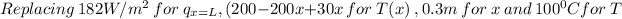 We have:
We have:
182 = h(200-200×0.3 + 30 ×0.3² - 100 )
182 = h (42.7)
h = 4.26 W/m².K
Thus, the convection coefficient is h = 4.26 W/m².K