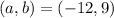Answer:
Center is

Explanation:
Given: Equation of a circle is
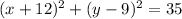
To find: center of the circle
Solution:
A circle is a locus of all points which are at equidistant from the fixed point (center).
Equation of a circle is of form
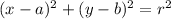 where
where
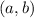 represents center of the circle and r denotes radius of the circle.
represents center of the circle and r denotes radius of the circle.
Given equation is
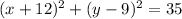
![\left [ x-(-12) \right ]^2+(y-9)^2=35](https://img.qammunity.org/2021/formulas/mathematics/college/16trhggnvklujrqwum7yuabdtxx8p40jk5.png)
Compare this equation with
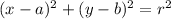
Center is