Answer:
the standard error of the proportion is 0.0272
Explanation:
We have that if the sample size is greater than 5% of the entire population, a finite population correction factor (fpc) is multiplied with the standard error :
fpc =
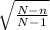
We know that N = 250 n = 91, replacing:
fpc =
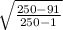
fpc = 0.799
Now, the formula would then be:
SE =
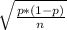 *fpc
*fpc
Now replacing, knowing that p = 0.12
SE=
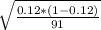 *0.799
*0.799
SE = 0.0272
So the standard error of the proportion is 0.0272