Answer:
(The diagram of the question is given in Attachment 1)
The largest load which can be applied is:
P=67.62 kN
Step-by-step explanation:
Make a Free body Diagram:
All the forces are shown in the diagram in Attachment 2.
Analyze the equilibrium of Joint C in Figure (a):
∑ F(y)= 0 (Upwards is positive)
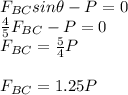
Substitute F(BC) in Figure (b):
∑ F(x)= 0 (Towards Right is positive)
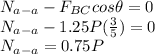
∑ F(y)= 0 (Upwards is positive)
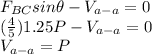
Find Cross Sectional Area:
The cross sectional area of a-a:
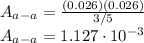
Find P from Normal Stress Equation:
σ = N(a-a)/A(a-a)
Substitute values:
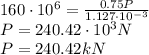
Find P from Shear Stress Equation:
Т= V(a-a)/A(a-a)
Substitute values:
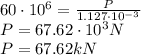
Results:
To satisfy both the condition, we have to choose the lower value of P.
P=67.62 kN