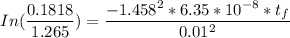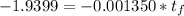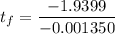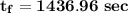Answer:
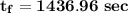
Step-by-step explanation:
Given that :
The strength and stability of tires may be enhanced by heating both sides of the rubber ( 0.14 W/m·K, 6.35 × 10^-8m^2/s)
i.e
k = 0.14 W/mK
∝ = 6.35 × 10⁻⁸ m²/s
L = 0.01 m
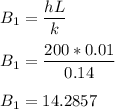
We cannot use the model of Lumped Capacitance; SO Let assume that Fourier Number
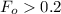
⇒

From Table 5.1 ; at
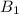 = 14.2857
= 14.2857
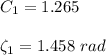
![(170-200)/(35-200) = 1.265 exp [ - (1.458)^2* ( \alpha t_f)/(L^2)]](https://img.qammunity.org/2021/formulas/engineering/college/m5kzl0rjsh5xbfaq66kjcluwf7lr58hvpj.png)