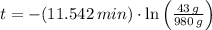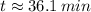Question

Element X decays radioactively with a half life of 8 minutes. If there are 980 grams of Element X, how long, to the nearest tenth of a minute, would it take the element to decay to 43 grams?

y=a(.5)^t/h

​

Answer 1

`t \approx 36.1\,min`

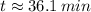
Explanation:

The time constant for the isotope decay is:

`\tau = (8\min)/(\ln 2)`

`\tau \approx 11.542\,min`

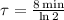
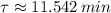
Now, the decay of the isotope is modelled after the following expression:

`m (t) = m_(o)\cdot e^{-(t)/(\tau) }`

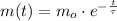
The time is now cleared with some algebraic handling:

`(m(t))/(m_(o)) = e^{-(t)/(\tau) }`

`t = -\tau \cdot \ln (m(t))/(m_(o))`

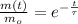
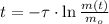
Finally, the time need for the element X to decay to 43 grams is:

`t = - (11.542\,min)\cdot \ln\left((43\,g)/(980\,g) \right)`

`t \approx 36.1\,min`