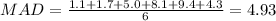Question

Find and interpret the mean absolute deviation of the data. Round your answers to the nearest tenth. If necessary 101.5 98.7 95.4 92.3 109.8 104.7

Answer 1

`\bar X = 100.4`

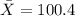
And we can calculate the deviations from each value like this:

`|101.5-100.4 |=1.1`

`|98.7-100.4 |=1.7`

`|95.4-100.4 |=5.0`

`|92.3-100.4 |=8.1`

`|109.8-100.4 |=9.4`

`|104.7-100.4|=4.3`

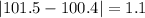
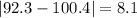
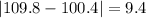
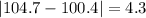
And the mean absolute deviation would be:

`MAD =(1.1+1.7+5.0+8.1+9.4+4.3)/(6)= 4.93`

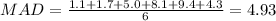
Explanation:

For this case we have the following dataset given:

101.5 98.7 95.4 92.3 109.8 104.7

We can calculate the mean with the following formula:

`\bar X =(\sum_(i=1)^n X_i)/(n)`

And replacing we got:

`\bar X = 100.4`

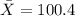
And we can calculate the deviations from each value like this:

`|101.5-100.4 |=1.1`

`|98.7-100.4 |=1.7`

`|95.4-100.4 |=5.0`

`|92.3-100.4 |=8.1`

`|109.8-100.4 |=9.4`

`|104.7-100.4|=4.3`

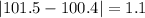
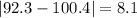
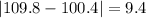
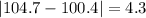
And the mean absolute deviation would be:

`MAD =(1.1+1.7+5.0+8.1+9.4+4.3)/(6)= 4.93`