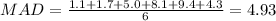Answer:
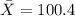
And we can calculate the deviations from each value like this:
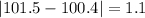
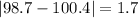
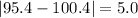
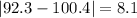
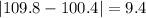
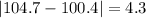
And the mean absolute deviation would be:
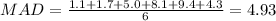
Explanation:
For this case we have the following dataset given:
101.5 98.7 95.4 92.3 109.8 104.7
We can calculate the mean with the following formula:
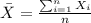
And replacing we got:
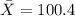
And we can calculate the deviations from each value like this:
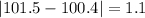
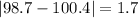
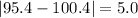
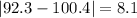
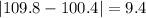
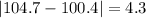
And the mean absolute deviation would be: