Question

Let (-3,5) be a point on the terminal side of theta. Find the exact values of sin theta, secant theta, and tangent theta

Can someone please help me out with this? If possible, providing a diagram would be helpful!

Answer 1

Cosθ = 0.5145

Sinθ = 0.8575

Secθ = 1.9436

tanθ = 1.667

Explanation:

From the figure attached,

Point P(-3, 5) is on the terminal side and AB is the initial side of the angle PAB.

If m∠PAB = θ

AB =
`\sqrt{(3)^(2)+(5)^(2)}`

=
`√(34)`

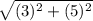
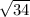
= 5.831

Then Cosθ =
`(AB)/(AP)` =
`(3)/(5.831)`

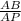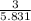
Cosθ = 0.5145

Sinθ =
`(PB)/(AP)`

Sinθ =
`(5)/(5.831)`

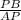
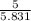
Sinθ = 0.8575

Secθ =
`\frac{1}{\text{Cos}\theta}`

Secθ =
`(1)/(0.5145)`

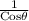
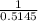
Secθ = 1.944

tanθ =
`(PB)/(AB)`

tanθ =
`(5)/(3)`

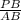
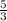
tanθ = 1.667