Question

In one area, monthly incomes of technology-related workers have a standard deviation of $650. It is believed that the standard deviation of the monthly incomes of non-technology workers is different. 71 non-technology workers are randomly selected and it is determined that these selected workers have a standard deviation of $950. Test the claim that the non-technology workers have a different standard deviation (so different from $650). Use a 0.10 significance level.

Answer 1

There is sufficient statistical evidence to prove that the standard deviation of the technology-related workers and the standard deviation of the non-technology workers are equal.

Explanation:

Here we have our null hypothesis as H₀: σ² = s²

Our alternative hypothesis is then Hₐ: σ² ≠ s²

We therefore have a two tailed test

To test the hypothesis of difference in standard deviation which is the Chi squared test given as follows

`\chi ^(2) = (\left (n-1 \right )s^(2))/(\sigma ^(2))`

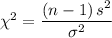
Where:

n = Size of sample

s² = Variance of sample = 950²

σ² = Variance of population = 650²

Degrees of freedom = n - 1 = 71 - 1 = 70

α = Significance level = 0.1

Therefore, we use 1 - 0.1 = 0.9

From the Chi-square table, we have the critical value as

1 - α/2 = 51.739,

α/2 = 90.531

Plugging the values in the above Chi squared test equation, we have;

`\chi ^(2) = (\left (23-1 \right )950^(2))/(650 ^(2)) = 49.994`

Therefore, since the test value within the critical region, we do not reject the null hypothesis, hence there is sufficient statistical evidence to prove that the standard deviation of the technology-related workers and the standard deviation of the non-technology workers are equal.