Question

In order to accurately estimate the difference between the number of touchdowns scored by the Detroit Lions and the Seattle Seahawks in a particular string of n = 5 games, we must know that the standard deviations for the two teams are equal. Suppose that in this string of games the Lions score an average of x_1 = 2 touchdowns per game with a standard deviation of s_1 = 0.37, while the Seahawks score an average of x_2 = 2.8 touchdowns with standard deviation s_2 = 1.89. Can we assume, at the alpha = 0.1 significance level, that the standard deviations for these two teams are the same? 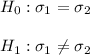a) Test Statistic: b) Critical Value: c) Conclusion: A. There is sufficient evidence to conclude that the standard deviations are different. B. There is insufficient evidence to conclude the standard deviations are different. We may assume they are equal.

Answer 1

Explanation:

Here,

`H_0:\sigma _1 = \sigma _2\\\\H_1:\sigma_1 \\eq \sigma_2`

a) Test Statistic

`F = (S_1^2)/(S_1^2) \\\\=(0.37^2)/(1,89^2) \\\\=0.04`

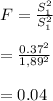
b) Critical value for

`\sigma = 0.1`

degrees of freedom is

`(n_1 - 1, n_2 -1)`

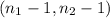
d.f =(5 - 1, 5 - 1)

d.f = (4, 4)

Fcritical=

`F_(0.1),(4,4)\\\\`

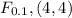
Fcritical = 4.11

Critical value = 4.11

Here,

F test Statistic < critical value

so we fail to reject null hypothesis H₀

Conclusion

There is insufficient evidence to conclude the standard deviations are different.

we may assume they are equal.