Question

There are many cylinders for which the height and radius are the same value. Let

c
c
represent the height and radius of a cylinder and
V
V
represent the volume of the cylinder.

Write an equation that expresses the relationship between the volume, height, and radius of this cylinder using c and V.
If the value of c is halved, what must happen to the value of the volume V?

Answer 1

Relation between V and c is represented as:

`V = \pi c^(3)`

When c is halved, V becomes
`(1)/(8)` of its initial value.

Explanation:

Height of cylinder = Radius of cylinder = c

Volume of cylinder = V

As per formula:

`V = \pi r^(2) h`

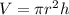
Where
`r` is the radius of cylinder and

`h` is the height of cylinder

Putting
`r = h =c`

`V = \pi c^(2) * c\\\Rightarrow V = \pi c^(3) ......(1)`

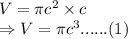
The values of c is halved:

Using equation (1), New volume:

`V' = \pi ((c)/(2))^3\\\Rightarrow (1)/(8) \pi c^(3)`

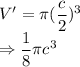
By equation (1), putting
`\pi * c^(3) = V`

`V' = (1)/(8) * V`

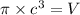
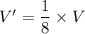
So, when c is halved, V becomes
`(1)/(8)` of its initial value.