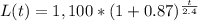Answer:
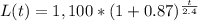
Explanation:
The locust population grows according to an exponential model with the following general formula:
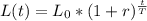
Where 'L0' is the initial locust population, 'r' is the increase rate after 'T' days, and 't' is the time passed, in days.
Applying the given data, the function that models the locust population t days since the first day of spring is: