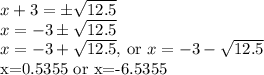Answer:
x=0.5355 or x=-6.5355
First step is to: Isolate the constant term by adding 7 to both sides
Explanation:
We want to solve this equation:
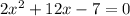
On observation, the trinomial is not factorizable so we use the Completing the square method.
Step 1: Isolate the constant term by adding 7 to both sides
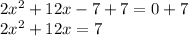
Step 2: Divide the equation all through by the coefficient of
 which is 2.
which is 2.
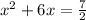
Step 3: Divide the coefficient of x by 2, square it and add it to both sides.
Coefficient of x=6
Divided by 2=3
Square of 3=
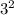
Therefore, we have:
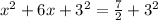
Step 4: Write the Left Hand side in the form
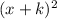
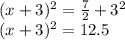
Step 5: Take the square root of both sides and solve for x