Answer:
Second quadrant = 120°.
Third quadrant = 210°
Explanation:
We are given that:
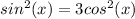
The following property is known:
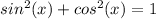
Combining both expressions:
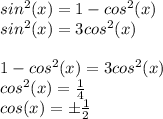
If x lies in the second quadrant, then cos(x) = -1/2:
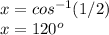
The value of x that satisfies the equation if x lies in the second quadrant is 120°.
If x lies in the third quadrant, then cos(x) = -1/2:
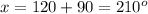
The value of x that satisfies the equation if x lies in the third quadrant is 210°