Answer:
Central angle of θ
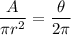
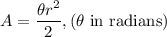
Explanation:
Suppose a sector of a circle with radius r has a central angle of θ.
Since a sector is a fraction of a full circle, the ratio of a sector's area A to the circle's area is equal to the ratio of the central angle of θ to the measure of a full rotation of the circle.
A full rotation of a circle is 2π radians.
This proportion can be written as:
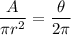
Multiply both sides by

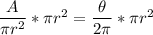
Simplify to get:
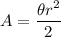
Where θ is the measure of the central angle of the sector and r is the radius of the circle.