Question

The chances of a tax return being audited are about 21 in 1 comma 000 if an income is less than​ $100,000 and 29 in 1 comma 000 if an income is​ $100,000 or more. Complete parts a through e. a. What is the probability that a taxpayer with income less than​ $100,000 will be​ audited? With income of​ $100,000 or​ more? Upper P (taxpayer with income less than $ 100 comma 000 is audited )equals nothing ​(Type an integer or a​ decimal.) What is the probability that a taxpayer with income of​ $100,000 or more will be​ audited? Upper P (taxpayer with income of $ 100 comma 000 or higher is audited )equals nothing ​(Type an integer or a​ decimal.) b. If five taxpayers with incomes under​ $100,000 are randomly​ selected, what is the probability that exactly one will be​ audited? That more than one will be​ audited?

Answer 1

a) p=0.021

b) p=0.029

c) Exactly one audit: P=0.0965

More than one audit: P=0.0042

Explanation:

a) If the income is less than $100,000, there is a probability of 21 in 1,000 of being audited. This is:

`p_1=(21)/(1,000)=0.021`

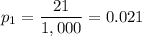
If the income is equal or more than $100,000, there is a probability of 29 in 1,000 of being audited. This is:

`p_2=(29)/(1,000)=0.029`

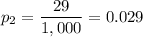
b) If we have 5 taxpayers with incomes under $100,000, and we want to know the probability that exactly one will be audited, we can model this a binomial randome variable, with p=0.021 and n=5:

`P(x=1) = \dbinom{5}{1} p^(1)q^(4)=5*0.021*0.9186=0.0965\\\\`

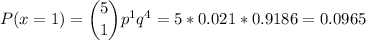
There is a probability of 0.0965 that exactly one out of a sample of five taxpayers with incomes under $100,000 will be audited.

To calculate the probability that more than one will be audited, we use the same distribution:

`P(x>1)=1-[P(x=0)+P(x=1)]\\\\\\P(x=0) = \dbinom{5}{0} p^(0)q^(5)=1*1*0.8993=0.8993\\\\\\P(x=1) = \dbinom{5}{1} p^(1)q^(4)=5*0.021*0.9186=0.0965\\\\\\P(x>1)=1-[P(x=0)+P(x=1)]\\\\P(x>1)=1-(0.8993+0.0965)\\\\P(x>1)=1-0.9958\\\\P(x>1)=0.0042`

There is a probability of 0.0042 that more than one out of a sample of five taxpayers with incomes under $100,000 will be audited.