Answer: 6.28 inches.
Explanation:
Formula :
i) Area of sector :
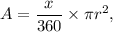 , where x = central angle and r is radius
, where x = central angle and r is radius
ii) Length of arc :
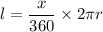
Given , r= 6 in.
A =
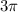 inches
inches
Put these values in (i) , we get
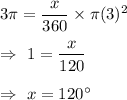
Now , put values of x and r in (ii) , we get
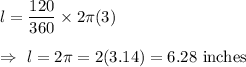
Hence, the length of the arc is 6.28 inches.