Question

The sector has an area of 3 pi inches squared and a radius of 6 in. How many inches long is the arc for this sector? Use 3.14 for Pi and round to the nearest hundredth.

A sector with a radius of 6 inches and area of 3 pi inches squared.

Recall that Area of a sector = StartFraction n degrees over 360 degrees EndFraction (pi) (r squared) and StartFraction Arc length over Circumference EndFraction = StartFraction n degrees over 360 degrees EndFraction.
3.14
6.28
12.56
18.84

Answer 1

6.28

Explanation:

Edge 2021

Answer 2

Answer: 6.28 inches.

Explanation:

Formula :

i) Area of sector :
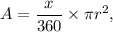`A=(x)/(360)*\pi r^2,`, where x = central angle and r is radius

ii) Length of arc :
`l=(x)/(360)*2\pi r`

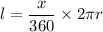
Given , r= 6 in.

A =
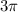`3\pi` inches

Put these values in (i) , we get

`3\pi =(x)/(360)*\pi (3)^2\\\\\Rightarrow\ 1=(x)/(120)\\\\\Rightarrow\ x=120^(\circ)`

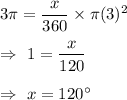
Now , put values of x and r in (ii) , we get

`l=(120)/(360)*2\pi(3)\\\\\Rightarrow\ l=2\pi = 2(3.14)=6.28\text{ inches}`

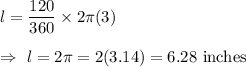
Hence, the length of the arc is 6.28 inches.