Question

Use the given values of n and p to find the minimum usual value μ - 2σ and the maximum usual value μ + 2σ.

n = 2136, p = 3/7


Answers:

1. Minimum: 843.1; maximum: 987.75

2. Minimum: 961.17; maximum: 869.69

3. Minimum: 892.56; maximum: 938.3

4. Minimum: 869.69; maximum: 961.17

Answer 1

`\mu -2\sigma = 915.428 - 2* 22.87=869.69`

`\mu +2\sigma = 915.428 + 2* 22.87=961.17`

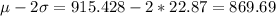
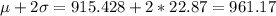
And the best option would be:

4. Minimum: 869.69; maximum: 961.17

Explanation:

We can assume that the variable of interst X is distributed with a binomial distribution and we can use the normal approximation.

For this case the mean would be given by:

`E(X) = np = 2136 *((3)/(7))= 915.428`

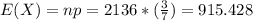
And the standard deviation would be:

`\sigma = \sqrt{2136*((3)/(7)) (1-(3)/(7))} =22.87`

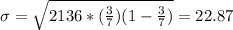
And if we find the limits we got:

`\mu -2\sigma = 915.428 - 2* 22.87=869.69`

`\mu +2\sigma = 915.428 + 2* 22.87=961.17`

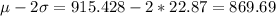
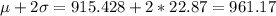
And the best option would be:

4. Minimum: 869.69; maximum: 961.17