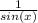Question

Cosx(tanx+cotx)=

Pls Help

Answer 1

final answer to the expression is csc(x)

Answer 2

Explanation:

Tangent is equal to sine over cosine. Cotangent is equal to cosine over sine. Therefore:

`cos(x)( (sin(x))/(cos(x)) + (cos(x))/(sin(x)) )`

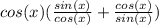
Distribute the cos(x) into the sum to get:

`sin(x) + \frac{ {cos(x)}^(2) }{sin(x)}`

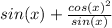
Get a common denominator by multiplying the first term by sine over sine to get:

`\frac{ {sin(x)}^(2) }{sin(x)} + \frac{ {cos(x)}^(2) }{sin(x)}`

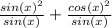
The numerator adds to equal 1 due to a common trigonometric identity. Therefore the only remaining term is:

`(1)/(sin(x))`