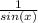Explanation:
Tangent is equal to sine over cosine. Cotangent is equal to cosine over sine. Therefore:
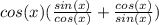
Distribute the cos(x) into the sum to get:

Get a common denominator by multiplying the first term by sine over sine to get:
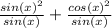
The numerator adds to equal 1 due to a common trigonometric identity. Therefore the only remaining term is: