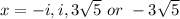2 Answers

Robou · Answer 1 · 2021-09-14T22:53:24+0000

Answer:

The correct answer is option

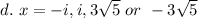
$d.\ x=-i, i, 3 √(5)\ or\ -3 √(5)$

Explanation:

The given equation has a degree 4 (Highest power of
):

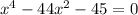x^4-44x^2-45=0 is the given equation which can be written as:

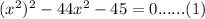
(x^2)^2-44x^2-45=0 ...... (1)

Let
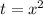t=x^(2) and putting it in equation (1):

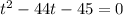
$t^2-44t-45=0 \\$

Solving the above quadratic equation in variable
:

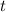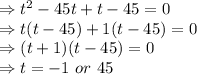
$\Rightarrow t^2-45t+t-45=0 \\\Rightarrow t(t-45)+1(t-45)=0\\\Rightarrow (t+1)(t-45)=0\\\Rightarrow t =-1\ or\ 45$

We know that
t=x^(2)

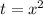
So,
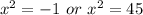
$x^(2) =-1\ or\ x^(2)= 45$

1. Solving
x^(2) =-1

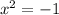
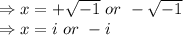
$\Rightarrow x = +√(-1)\ or\ -√(-1)\\\Rightarrow x = i\ or\ -i$

2. Solving
x^(2) =45

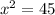
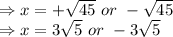
$\Rightarrow x = +√(45)\ or\ -√(45)\\\Rightarrow x = 3√(5)\ or\ -3√(5)$

Hence, correct answer is:

$x=-i, i, 3 √(5)\ or\ -3 √(5)$

Please log in or register to add a comment.