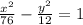Answer:
The equation of the hyperbola is:
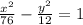
Explanation:
The equation of a hyperbola centered in the origin in standard form is:

The distance between both vertexes is equal to:
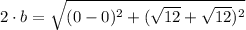
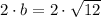
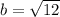
Now, the distance between any of the vertexes and origin is:
![c = \sqrt{(0-0)^(2)+[(4-(-4)]^(2)}](https://img.qammunity.org/2021/formulas/mathematics/college/btaoaj7f3stxe2d23gs874r481wxpr2nzk.png)
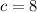
The remaining parameter of the hyperbola is determined by the following Pythagorean expression:
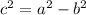
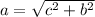

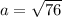
The equation of the hyperbola is: