Question

Write the equation of the line that passes through the points (2,-4) and (4,2) in slope-intercept form.

Answer 1

Slope Intercept Form: y=3x-10

Explanation:

First, we need to solve the slope.

The formula: y2-y1/x2-x1 = m

Coordinate Points:

(2, -4) ; (4,2)

Do 2 - (-4) for the y's and 4-2 for the x's

Formula: 2-(-4)/4-2

2 - (-4) is a positive answer since the negatives cancel to a positive.

That shall be 6.

4-2 = 2

Now we have 6/2 which means 6 divided by 2 which is 3.

Our slope is 3.

Slope-Intercept Formula: y=mx+b

Our "m" is 3

y = 3x + b

Our b which is the y-intercept is undefined.

We need to plug one of the coordinates into the formula to find it.

Plug (2,-4) into the formula.

-4 = 3(2) +b

Do 3 x 2 first

-4 = 6 + b

Now subtract 6 on both sides

-6-4 = b

Our y-intercept is -10 because negative subtracted by negatives is an addition number followed by the greater number's sign.

Formula: y=3x-10

Answer 2

y = 3x - 10

Explanation:

To determine the line that passes through the points (2, -4) and (4, 2), we need to determine the slope of the line. Then, using the slope of the line and any point, we can determine the equation of the line using point slope form.

How to determine the slope of the line?

The slope of the line can be determined by using the formula (y₂ - y₁)/(x₂ - x₁), where x₂ and y₂ are the coordinates of the second point; x₁ and y₁ are the coordinates of the first point.

Determining the slope of the line:

`\implies\large\text{Slope} = (y_(2) - y_(1) )/(x_(2) - x_(1) )`

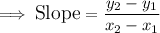
In this case, our first point and second point are (2, -4) and (4, 2) repectively as stated in the question. Therefore,

• Point₁ = (x₁, y₁) = (2, -4) ⇒ x₁ = 2 y₁ = -4
• Point₂ = (x₂, y₂) = (4, 2) ⇒ x₂ = 4 y₂ = 2

When we substitute the following into the formula, we obtain;

`\implies\large\text{Slope} = (2- (-4))/(4 - 2 )`

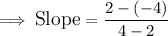
When we perform subtraction, we obtain;

`\implies\large\text{Slope} = (2- (-4))/(4 - 2 ) = (2 + 4)/(2 ) = (6)/(2)`

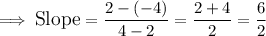
Which when simplified, we get;

`\implies\large\text{Slope} = (6)/(2) = 3`

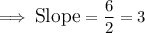
Determining the equation of the line:

As said above, to determine the equation of the line with the slope and a point given, we can use point slope form. The chosen point must be on the line. The question states that "the line that passes through the points (2,-4) and (4, 2)". Therefore, we can tell that (2,-4) and (4, 2) are points that are on the line. Let's choose (4, 2) as our chosen point.

• Chosen point: (4, 2)

Now, let's substitute the slope of the line and the coordinates of the chosen point in the point slope form equation.

• ⇒ Point slope form: y - y₁ = m(x - x₁)
• ⇒ Point slope form: y - 2 = 3(x - 4)

Finally, let's simplify the point slope equation and convert it into slope intercept form (as stated in question).

• ⇒ Point slope form: y - 2 = 3x - 12

The slope intercept form states that;

• Slope intercept form: y = (m)x + (b)

We can see that the "y" variable is isolated on one side of the equation [y = (m)x + (b), Slope intercept form equation]. Thus, we need to isolate the y-variable in y - 2 = 3x - 12 to obtain our equation in slope intercept form. This can be done by adding 2 to both sides of the equation.

• ⇒ y - 2 + 2 = 3x - 12 + 2
• ⇒ y = 3x - 10

Therefore, the equation in slope intercept form is y = 3x - 10.