Question

calculate the missing length on the right triangle solve for c using the z y t h a g o r e a n t h e o r e m a2 plus B2 equals C2

Answer 1

Explanation:

Since the diagram to this question is not given ; we will just explain the concept of the right angled triangle and a means by which we can use the Pythagoras theorem in solving such related question.

A right angled triangle has to legs which serves as the base line in which the height of the right angle is 90°.

Now; If we have a base line AB; let say , we chose any convenient radius at a and bisect an arc. at the arc we make another arc to the right ; we will have an angle at A which is 60°, So B will form a straight line up serving the role of the right angle which is 90° and where both met will be C which is 30°

So now we have a triangle ABC, if the line facing ∠ A = a ; the line facing ∠ B = b and the line facing ∠ C = c

Then; we can solve for side c if ; side a and side b are known by using the Pythagoras theorem.

Using Pythagoras theorem.

a² = b² + c²

-c² = b² - a²

Multiplying through with -

c² = - b² + a²

`\mathbf{ c = √(-b^2 + a^2)}`

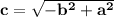
Since ; we already make c the subject of the formula; from the missing diagram, we can easily slot the values of a and b given to solve for the value of c using the above derived equation.

I hope that helps!.