Final Answer:
The equation of the graph that represents the reflection of
 about the origin is
about the origin is
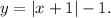
Step-by-step explanation:
To find the equation of the graph that represents the reflection of
 about the origin, we'll determine how the graph of the function
about the origin, we'll determine how the graph of the function
 changes due to the reflection across the origin.
changes due to the reflection across the origin.
The graph
 is a reflection of the absolute value function
is a reflection of the absolute value function
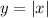 over the x-axis, shifted one unit to the right and down by one unit. When reflecting a graph about the origin, both the x and y values change signs.
over the x-axis, shifted one unit to the right and down by one unit. When reflecting a graph about the origin, both the x and y values change signs.
For the original equation
 to reflect it across the origin, the negative sign before the absolute value is reversed to a positive sign. Hence,
to reflect it across the origin, the negative sign before the absolute value is reversed to a positive sign. Hence,
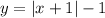 represents the reflected graph.
represents the reflected graph.
The transformation from
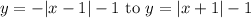 involves replacing
involves replacing
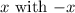 to reflect the graph over the y-axis and changing the constant term from
to reflect the graph over the y-axis and changing the constant term from
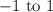 to reflect it over the x-axis. This results in the equation
to reflect it over the x-axis. This results in the equation
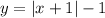 , representing the graph of the function reflected about the origin.
, representing the graph of the function reflected about the origin.