Answer:
The standard deviation for the given data set is 1.65.
Explanation:
The Standard Deviation is defined as
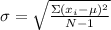
Where
 is the standard deviation,
is the standard deviation,
 is the mean and
is the mean and
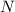 is the total number of data.
is the total number of data.
So, first, we need to find the mean of the data set.
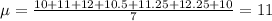
Now, we have to subtract each data with the mean to then elevate the differnece to the square power.
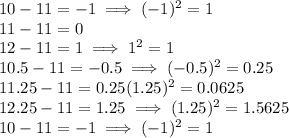
Then, we sum all these results.
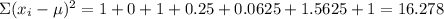
Next, we divide the sum by
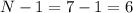
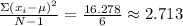
Finally, we apply the square root.
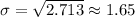
Therefore, the standard deviation for the given data set is 1.65.