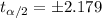Answer:
a)
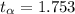
b)

c)
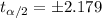
Explanation:
Part a
For this case we know that the degrees of freedom are:
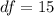
And we want a right tailed test so then we need to find in the t distribution with degrees of freedom =15 a critical value who accumulate 0.05 of the area in the right and we got:
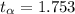
Part b
For this case the significance is
 the degrees of freedom are:
the degrees of freedom are:
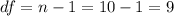
And since is a left tailed test the critical value for this case would be:

Part c
For this case the significance is
 and
and
 the degrees of freedom are:
the degrees of freedom are:
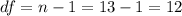
And since is a two tailed test the critical values for this case would be: