Answer:
Sharing cone holds 9 times more popcorn than a skinny cone.
Explanation:
Height of each cone = 9 inches
Radius of the sharing size cone = 3 times radius of the skinny size cone
Let the radius of skinny size cone = r
Then radius of the sharing size cone = 3r
Volume of the sharing size cone =
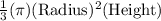
=

= 27πr²
Volume of the skinny size cone =
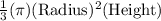
=

= 3πr²
Ratio of the volumes =

=
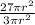
= 9
Therefore, sharing cone holds 9 times more popcorn than a skinny cone.