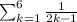Question

Help with this question asap!!

Answer 1

1st option.

`\sum_(k=1)^(6) (1)/(2k-1)`

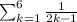
Explanation:

The given sequence is as follows:

`1 + (1)/(3)+ (1)/(5)+ (1)/(7)+ (1)/(9)+ (1)/(11)`

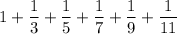
Here, we can see that the denominator is in AP and the sequence is:

1, 3, 7, 9, 11

first term, a = 1

Common difference, d = 2

We know that nth term for an AP:

`a_n = a+(n-1)d`

where a is the first term and

d is the common difference.

So, nth term for above AP:

`a_n = 1+(n-1)* 2\\\Rightarrow 2n-1`

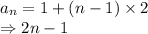
Here, we have 'k' in place of 'n':

`a_k = 2k-1`

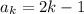
And as per the given sequence in the question, the kth term is simply the reciprocal:

i.e.
`(1)/(2k-1)`

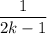
and sum is to be done up to k = 6 from k = 1.

Hence, the summation notation for the sequence

`1 + (1)/(3)+ (1)/(5)+ (1)/(7)+ (1)/(9)+ (1)/(11)`

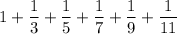
is:

`\sum_(k=1)^(6) (1)/(2k-1)`