Answer:
8 units
Explanation:
Hello!
So, there's a formula we can apply to right-angled triangles: Pythagorean's theorem. It states that c =
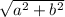 , where c is the hypotenuse and a and b are the legs of the triangle.
, where c is the hypotenuse and a and b are the legs of the triangle.
So, from the problem, if c = 17 and a = 15, then, we're solving for b. So we'll rewrite the theorem to solve for b.
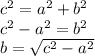
Okay, so now we have isolated the theorem for b. Let's plug in our values for c and a.

So, using the theorem, we found b = 8. To check our work, let's plug in b and a and solve for c.
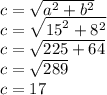
So, we got our hypotenuse to equal 17 units, which is correct! So, our b is correct too. Awesome