Answer:
The distance from station A to the fire is 90.4 miles
The distance from station B to the fire is 95.6 miles
Explanation:
Given that 2 fire stations are 100 miles apart.
Station A = N 55°E
Station B = S 60°E
To find the distance of the fire from each station, let's use the law of sines,
From the diagram, our values are:
A = 55°
B = 60°
Let's take C as point of fire.
Since the total sum of angle in a triangle is 180,
A+B+C=180
C = 180 - A - B
C = 180 - 55 - 60 = 65°
For station A.
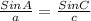

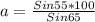
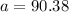
The distance from station A to the fire is 90.4 miles
For station B:
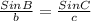

Solving for b, we have:
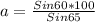
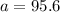
The distance from station B to the fire is 95.6 miles